Критерий независимости

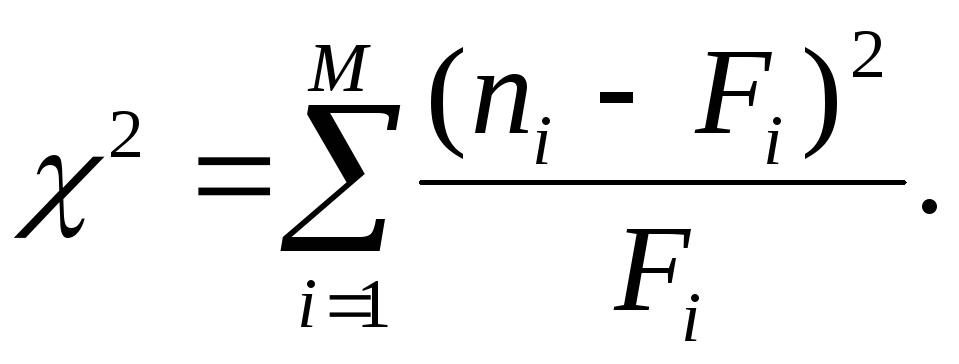
А сейчас будет самое вкусное — критерий независимости. Это будет самый сложный инструмент из всех, которые мы видели в предыдущих публикациях. Но его возможности очень велики и стоят потраченного времени! Критерий независимости идеально подходит для дискретных величин, с которыми обычно и сталкиваются астрологи во время исследований. Кроме того, он не требует предварительно определения закона распределения случайной величины. Он позволяет ответить на вопрос «А зависит ли одно явление от другого?» Например, зависит ли поведение от положения планеты. Готовы? Тогда давайте считать!

Первое, что нам нужно сделать, это построить таблицу сопряженности. По горизонтали и вертикали в такой таблице отмечаются признаки, зависимость или независимость которых нужно проверить. Столбцов должно быть меньше, чем строк — так принято. Для каждой строки и колонки подсчитывают сумму значений, а также удельный вес — сумму значений строки/столбца делят на сумму значений в таблице (сумму значений в выборке). Первая таблица готова, это таблица сопряженности наблюдаемых значений и дополнительные (вспомогательные) строки/столбцы с суммами и удельными весами.

Следующее, что нам нужно сделать, это построить таблицу ожидаемых значений. Эта таблица в точности дублирует таблицу наблюдаемых значений. Для неё не нужны дополнительные (вспомогательные) строки/столбцы, а значение каждой ячейки будет рассчитываться как произведение общего числа наблюдений (сумма значений в выборке), удельного веса строки и удельного веса столбца подсчитанных для таблицы наблюдаемых значений, соответствущие этой ячейке.

Все остальное за нас сделает машина. Любой вариант электронной таблицы поймёт и с радостью выполнит функцию =CHISQ.TEST(табл_наблюдаемых; табл_ожидаемых) — только данные наблюдений, без сумм и без удельных весов. Если полученное значение меньше уровня значимости (обычно он равен 0,05), то рассматриваемые факторы влияют друг на друга.